机器学习 - 决策树

决策树(Decision Tree)
在本章中,我们将向您展示如何制作“决策树”。决策树是一种流程图,可以帮助您根据以前的经验进行决策。
在这个例子中,一个人将尝试决定他/她是否应该参加喜剧节目。
幸运的是,我们的例中人物每次在镇上举办喜剧节目时都进行注册,并注册一些关于喜剧演员的信息,并且还登记了他/她是否去过。
| Age | Experience | Rank | Nationality | Go |
|---|---|---|---|---|
| 36 | 10 | 9 | UK | NO |
| 42 | 12 | 4 | USA | NO |
| 23 | 4 | 6 | N | NO |
| 52 | 4 | 4 | USA | NO |
| 43 | 21 | 8 | USA | YES |
| 44 | 14 | 5 | UK | NO |
| 66 | 3 | 7 | N | YES |
| 35 | 14 | 9 | UK | YES |
| 52 | 13 | 7 | N | YES |
| 35 | 5 | 9 | N | YES |
| 24 | 3 | 5 | USA | NO |
| 18 | 3 | 7 | UK | YES |
| 45 | 9 | 9 | UK | YES |
现在,基于此数据集,Python 可以创建决策树,这个决策树可用于决定是否值得参加任何新的演出。
工作原理
首先,导入所需的模块,并使用 pandas 读取数据集:
实例
读取并打印数据集:
import pandas
df = pandas.read_csv("data.csv")
print(df)
如需制作决策树,所有数据都必须是数字。
我们必须将非数字列 “Nationality” 和 “Go” 转换为数值。
Pandas 有一个 map() 方法,该方法接受字典,其中包含有关如何转换值的信息。
{'UK': 0, 'USA': 1, 'N': 2}
表示将值 'UK' 转换为 0,将 'USA' 转换为 1,将 'N' 转换为 2。
实例
将字符串值更改为数值:
d = {'UK': 0, 'USA': 1, 'N': 2}
df['Nationality'] = df['Nationality'].map(d)
d = {'YES': 1, 'NO': 0}
df['Go'] = df['Go'].map(d)
print(df)
然后,我们必须将特征列与目标列分开。
特征列是我们尝试从中预测的列,目标列是具有我们尝试预测的值的列。
实例
X 是特征列,y 是目标列:
features = ['Age', 'Experience', 'Rank', 'Nationality'] X = df[features] y = df['Go'] print(X) print(y)
现在我们可以创建实际的决策树,并用我们的数据进行拟合。首先导入所需模块:
实例
创建并展示决策树:
import pandas
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
df = pandas.read_csv("data.csv")
d = {'UK': 0, 'USA': 1, 'N': 2}
df['Nationality'] = df['Nationality'].map(d)
d = {'YES': 1, 'NO': 0}
df['Go'] = df['Go'].map(d)
features = ['Age', 'Experience', 'Rank', 'Nationality']
X = df[features]
y = df['Go']
dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
tree.plot_tree(dtree, feature_names=features)
结果解释
决策树使用您先前的决策来计算您是否愿意去看喜剧演员的几率。
让我们阅读决策树的不同方面:

Rank
Rank <= 6.5 表示排名在 6.5 以下的喜剧演员将遵循 True 箭头(向左),其余的则遵循 False 箭头(向右)。
gini = 0.497 表示分割的质量,并且始终是 0.0 到 0.5 之间的数字,其中 0.0 表示所有样本均得到相同的结果,而 0.5 表示分割完全在中间进行。
samples = 13 表示在决策的这一点上还剩下 13 位喜剧演员,因为这是第一步,所以他们全部都是喜剧演员。
value = [6, 7] 表示在这 13 位喜剧演员中,有 6 位将获得 "NO",而 7 位将获得 "GO"。
Gini
分割样本的方法有很多,我们在本教程中使用 GINI 方法。
基尼方法使用以下公式:
Gini = 1 - (x/n)2 - (y/n)2
其中,x 是肯定答案的数量 ("GO"),n 是样本数量,y 是否定答案的数量 ("NO"),使用以下公式进行计算:
1 - (7 / 13)2 - (6 / 13)2 = 0.497

下一步包含两个框,其中一个框用于喜剧演员,其 'Rank' 为 6.5 或更低,其余为一个框。
True - 5 名喜剧演员在这里结束:
gini = 0.0 表示所有样本均得到相同的结果。
samples = 5 表示该分支中还剩下 5 位喜剧演员(5 位的等级为 6.5 或更低的喜剧演员)。
value = [5, 0] 表示 5 得到 "NO" 而 0 得到 "GO"。
False - 8 位戏剧演员继续:
Nationality(国籍)
Nationality <= 0.5 表示国籍值小于 0.5 的喜剧演员将遵循左箭头(这表示来自英国的所有人),其余的将遵循右箭头。
gini = 0.219 意味着大约 22% 的样本将朝一个方向移动。
samples = 8 表示该分支中还剩下 8 个喜剧演员(8 个喜剧演员的等级高于 6.5)。
value = [1, 7] 表示在这 8 位喜剧演员中,1 位将获得 "NO",而 7 位将获得 "GO"。

True - 4 名戏剧演员继续:
Age(年龄)
Age <= 35.5 表示年龄在 35.5 岁或以下的喜剧演员将遵循左箭头,其余的将遵循右箭头。
gini = 0.375 意味着大约 37.5% 的样本将朝一个方向移动。
samples = 4 表示该分支中还剩下 4 位喜剧演员(来自英国的 4 位喜剧演员)。
value = [1, 3] 表示在这 4 位喜剧演员中,1 位将获得 "NO",而 3 位将获得 "GO"。
False - 4 名喜剧演员到这里结束:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 4 表示该分支中还剩下 4 位喜剧演员(来自英国的 4 位喜剧演员)。
value = [0, 4] 表示在这 4 位喜剧演员中,0 将获得 "NO",而 4 将获得 "GO"。

True - 2 名喜剧演员在这里结束:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 2 表示该分支中还剩下 2 名喜剧演员(2 名 35.5 岁或更年轻的喜剧演员)。
value = [0, 2] 表示在这 2 位喜剧演员中,0 将获得 "NO",而 2 将获得 "GO"。
False - 2 名戏剧演员继续:
Experience(经验)
Experience <= 9.5 表示具有 9.5 年或以上经验的喜剧演员将遵循左侧的箭头,其余的将遵循右侧的箭头。
gini = 0.5 表示 50% 的样本将朝一个方向移动。
samples = 2 表示此分支中还剩下 2 个喜剧演员(2 个年龄超过 35.5 的喜剧演员)。
value = [1, 1] 表示这两个喜剧演员中,1 将获得 "NO",而 1 将获得 "GO"。
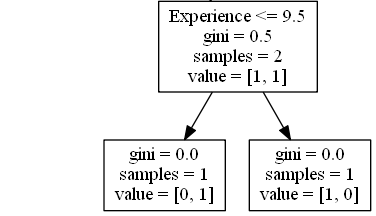
True - 1 名喜剧演员在这里结束:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 1 表示此分支中还剩下 1 名喜剧演员(1 名具有 9.5 年或以下经验的喜剧演员)。
value = [0, 1] 表示 0 表示 "NO",1 表示 "GO"。
False - 1 名喜剧演员到这里为止:
gini = 0.0 表示所有样本都得到相同的结果。
samples = 1 表示此分支中还剩下 1 位喜剧演员(其中 1 位具有超过 9.5 年经验的喜剧演员)。
value = [1, 0] 表示 1 表示 "NO",0 表示 "GO"。
预测值
我们可以使用决策树来预测新值。
例如:我是否应该去看一个由 40 岁的美国喜剧演员主演的节目,该喜剧演员有 10 年的经验,喜剧排名为 7?
实例
使用 predict() 方法来预测新值:
print(dtree.predict([[40, 10, 7, 1]]))
实例
如果喜剧等级为 6,答案是什么?
print(dtree.predict([[40, 10, 6, 1]]))
不同的结果
如果运行足够多次,即使您输入的数据相同,决策树也会为您提供不同的结果。
这是因为决策树无法给我们 100% 的肯定答案。它基于结果的可能性,答案会有所不同。